Uji kompetensi 4 adalah akhir dari Bab Persamaan garis lurus yang terdapat dalam Buku Matematika Kelas 8 Kurikulum 2013 Revisi 2017 Semester 1. Uji kompetensi 4 terdapat pada halaman 181 - 188.
Seperti uji kompetensi lainnya, uji kompetensi 3 ini terdiri dari 2 bagian yaitu pilihan ganda dan esai. Pilihan ganda terdiri dari 20 nomor soal sedangkan esai ada 11 nomor. Pada artikel kali ini akan membahas bagian pilihan gandanya saja. Bagian Esai akan dibahas pada artikel selanjutnya ya!
1. Persamaan berikut yang termasuk persamaan garis lurus adalah ....
Kunci jawaban: 2y + 4x = 0
2. Gradien garis yang memiliki persamaan y = 2x + 3 adalah ....
Kunci jawaban : 2
Baca juga : Soal Uji Kompetensi 4 Bab Persamaan Garis Lurus Kelas 8 Semester 1 Kurikulum 2013 Revisi 2018
3. Titik yang terletak pada persamaan 4x - 2y - 2 = 0 adalah ....
Kunci jawaban : (2,3)
4. Gradien garis dengan persamaan 2x + 4y + 4 = 0 adalah ....
Kunci jawaban : -1/2
5. Gradien garis dengan persamaan 4x - 2y - 7 = 0 adalah ....
Kunci jawaban : 2
6. Gradien garis AB adalah ....
Kunci jawaban : -1/2
7. Titik (-5,5) melalui persamaan garis ....
Kunci jawaban : 3x + 2y = -5
8. Persamaan garis yang melalui titik (-5,4) dan memiliki gradien -3 adalah ....
Kunci jawaban : y +3x = - 11
9. Titik (3, 4) dilalui persamaan garis ....
Kunci jawaban : tidak ada jawaban yang benar
10. Gradien garis yang melalui titik (1, 2) dan titik (3, 4) adalah ....
Kunci jawaban : 1
11. Persamaan suatu garis yang melalui titik (1, 2) dan titik (3, 4) adalah ....
Kunci jawaban : y = x + 1
12. Persamaan garis yang melalui titik (3, 6) dan sejajar dengan garis 2y + 2x = 3 adalah ....
Kunci jawaban : y = -x + 9
13. Persamaan garis yang melalui titik (-3,6) dan sejajar dengan garis 4y - 3x = 5 adalah ....
Kunci jawaban : tidak ada jawaban yang memenuhi
Jawaban alternatif : 4y = - 3x + 15
14. Persamaan garis yang melalui titik (4, –3) dan tegak lurus dengan garis 4y – 6x +10 = 0 adalah ....
Kunci jawaban : tidak ada jawaban yang memenuhi
Jawaban alternatif : 3y + 2x = - 1
15. Garis yang melalui titik (5, –3) dan sejajar dengan garis yang mempunyai gradien 1/3 adalah ....
Kunci jawaban :
16. Garis yang melalui titik (5, –3) dan tegak lurus pada garis yang mempunyai gradien – 2/3 adalah ....
Kunci jawaban :
17. Persamaan garis lurus yang melalui titik (–2, –4) dan titik (–4, 3) adalah ....
Kunci jawaban :
18. Persamaan garis yang melalui titik (4, 6) dan sejajar dengan garis yang melalui titik (3, 4) dan titik (5, 1) adalah ....
Kunci jawaban :
19. Persamaan garis yang melalui titik (6, –4) dan sejajar dengan garis yang melalui titik (–7, –4) dan titik (5, –5) adalah ....
Kunci jawaban :
20. Persamaan garis yang melalui titik (0, 6) dan tegak lurus dengan garis yang melalui titik (–4, 5) dan titik (–3, 3) adalah ....
Demikian Kunci Jawaban Uji Kompetensi 4 Bab Persamaan Garis Lurus Matematika Kelas 8 Semester 1. Semoga bermanfaat.
Seperti uji kompetensi lainnya, uji kompetensi 3 ini terdiri dari 2 bagian yaitu pilihan ganda dan esai. Pilihan ganda terdiri dari 20 nomor soal sedangkan esai ada 11 nomor. Pada artikel kali ini akan membahas bagian pilihan gandanya saja. Bagian Esai akan dibahas pada artikel selanjutnya ya!
Kalau anda membutuhkan file ini maka tinggalkan jejak email anda di komentar ya! Kami akan berusaha segera mengirimkannya ke email anda.
Kunci Jawaban Uji Kompetensi 4 Bab Persamaan Garis Lurus Matematika Kelas 8 Semester 1
Pilihan Ganda1. Persamaan berikut yang termasuk persamaan garis lurus adalah ....
Kunci jawaban: 2y + 4x = 0
Pembahasan:
Persamaan umum garis lurus adalah y = mx + c yang memiliki dua variabel yakni x dan y dimana setiap variabel berderajat 1.
Persamaan 2y + 4x = 0 merupakan persamaan linier dua variabel yang dapat diubah ke bentuk persamaan garis lurus seperti berikut.
2y + 4x = 0
2y = -4x
y = (-4/2)x
y = -2x
Selesai...
Persamaan umum garis lurus adalah y = mx + c yang memiliki dua variabel yakni x dan y dimana setiap variabel berderajat 1.
Persamaan 2y + 4x = 0 merupakan persamaan linier dua variabel yang dapat diubah ke bentuk persamaan garis lurus seperti berikut.
2y + 4x = 0
2y = -4x
y = (-4/2)x
y = -2x
Selesai...
2. Gradien garis yang memiliki persamaan y = 2x + 3 adalah ....
Kunci jawaban : 2
Pembahasan:
Persamaan umum garis lurus adalah y = mx + c
Sehingga persamaan y = 2x + 3 merupakan persamaan garis lurus dengan gradien (m) = 2 dan konstanta (c) = 3.
Gradien bisa disebut juga dengan kemiringan atau koefisien arah.
Persamaan umum garis lurus adalah y = mx + c
Sehingga persamaan y = 2x + 3 merupakan persamaan garis lurus dengan gradien (m) = 2 dan konstanta (c) = 3.
Gradien bisa disebut juga dengan kemiringan atau koefisien arah.
Baca juga : Soal Uji Kompetensi 4 Bab Persamaan Garis Lurus Kelas 8 Semester 1 Kurikulum 2013 Revisi 2018
3. Titik yang terletak pada persamaan 4x - 2y - 2 = 0 adalah ....
Kunci jawaban : (2,3)
Pembahasan:
Koordinat titik yang berada pada garis harus memenuhi persamaan tersebut.
Koordinat (2,3) maka x = 2 dan y = 3 dimasukkan ke dalam persamaan, maka:
4x - 2y - 2 = 0
4.2 - 2.3 - 2 = 0
8 - 6 - 2 = 0
2 - 2 = 0
0 = 0
Karena nilai ruas kiri dan kanan sama-sama nol (0) maka benar koordinat (2,3) terletak pada persamaan 4x - 2y - 2 = 0.
Koordinat titik yang berada pada garis harus memenuhi persamaan tersebut.
Koordinat (2,3) maka x = 2 dan y = 3 dimasukkan ke dalam persamaan, maka:
4x - 2y - 2 = 0
4.2 - 2.3 - 2 = 0
8 - 6 - 2 = 0
2 - 2 = 0
0 = 0
Karena nilai ruas kiri dan kanan sama-sama nol (0) maka benar koordinat (2,3) terletak pada persamaan 4x - 2y - 2 = 0.
4. Gradien garis dengan persamaan 2x + 4y + 4 = 0 adalah ....
Kunci jawaban : -1/2
Pembahasan:
Persamaan umum garis lurus adalah y = mx + c
Persamaan 2x + 4y + 4 = 0 dapat diubah menjadi:
2x + 4y + 4 = 0
4y = -2x - 4
y = (-2x - 4)/4
y = (-2/4)x - (4/4)
y = (-1/2)x - 1
Persamaan y = (-1/2)x - 1 merupakan persamaan garis lurus dengan gradien (m) = -1/2 dan konstanta (c) = -1.
Persamaan umum garis lurus adalah y = mx + c
Persamaan 2x + 4y + 4 = 0 dapat diubah menjadi:
2x + 4y + 4 = 0
4y = -2x - 4
y = (-2x - 4)/4
y = (-2/4)x - (4/4)
y = (-1/2)x - 1
Persamaan y = (-1/2)x - 1 merupakan persamaan garis lurus dengan gradien (m) = -1/2 dan konstanta (c) = -1.
5. Gradien garis dengan persamaan 4x - 2y - 7 = 0 adalah ....
Kunci jawaban : 2
Pembahasan:
Persamaan umum garis lurus adalah y = mx + c
Persamaan 4x - 2y - 7 = 0 dapat diubah menjadi:
4x - 2y - 7 = 0
-2y = -4x + 7
y = (-4x + 7)/-2
y = (-4/-2)x + (7/-2)
y = 2x - 7/2
Persamaan y = 2x - 7/2 merupakan persamaan garis lurus dengan gradien (m) = 2 dan konstanta (c) = -7/2.
Persamaan umum garis lurus adalah y = mx + c
Persamaan 4x - 2y - 7 = 0 dapat diubah menjadi:
4x - 2y - 7 = 0
-2y = -4x + 7
y = (-4x + 7)/-2
y = (-4/-2)x + (7/-2)
y = 2x - 7/2
Persamaan y = 2x - 7/2 merupakan persamaan garis lurus dengan gradien (m) = 2 dan konstanta (c) = -7/2.
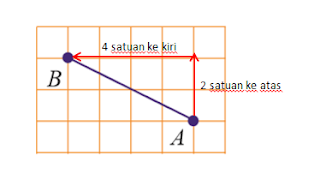
6. Gradien garis AB adalah ....
Kunci jawaban : -1/2
Pembahasan:
Gradien/kemiringan = perubahan panjang sisi tegak (y)/perubahan panjang sisi mendatar
Kemiringan suatu garis ditentukan oleh 2 buah titik pada garis tersebut.
ingat kembali aturan pada sistem koordinat bahwa:
Untuk mendapatkan kemiringan garis AB kita harus bergerak 2 satuan ke atas (searah sumbu Y) dan 4 satuan ke kiri (searah sumbu X) maka kemiringan garis AB adalah:
= perubahan panjang sisi tegak (y)/perubahan panjang sisi mendatar
= 2/(-4)
= -1/2
Jadi gradien garis AB adalah -1/2.
Gradien/kemiringan = perubahan panjang sisi tegak (y)/perubahan panjang sisi mendatar
Kemiringan suatu garis ditentukan oleh 2 buah titik pada garis tersebut.
ingat kembali aturan pada sistem koordinat bahwa:
- Melangkah ke kanan itu positif
- Melangkah ke atas itu positif
- Melangkah ke kiri itu negatif
- Melangkah ke bawah itu negatif
Untuk mendapatkan kemiringan garis AB kita harus bergerak 2 satuan ke atas (searah sumbu Y) dan 4 satuan ke kiri (searah sumbu X) maka kemiringan garis AB adalah:
= perubahan panjang sisi tegak (y)/perubahan panjang sisi mendatar
= 2/(-4)
= -1/2
Jadi gradien garis AB adalah -1/2.
7. Titik (-5,5) melalui persamaan garis ....
Kunci jawaban : 3x + 2y = -5
Pembahasan:
Masukkan titik (-5,5) ke masing-masing persamaan dengan x = -5 dan y = 5.
Persamaan yang memenuhi adalah 3x + 2y = -5 karena:
3x + 2y = -5
3.(-5) + 2.5 = -5
-15 + 10 = -5
-5 = -5
karena kedua ruas sama maka (-5,5) dilalui oleh garis 3x + 2y = -5.
Masukkan titik (-5,5) ke masing-masing persamaan dengan x = -5 dan y = 5.
Persamaan yang memenuhi adalah 3x + 2y = -5 karena:
3x + 2y = -5
3.(-5) + 2.5 = -5
-15 + 10 = -5
-5 = -5
karena kedua ruas sama maka (-5,5) dilalui oleh garis 3x + 2y = -5.
8. Persamaan garis yang melalui titik (-5,4) dan memiliki gradien -3 adalah ....
Kunci jawaban : y +3x = - 11
Pembahasan:
Rumus umum mencari persamaan garis dengan gradien m pada titik (x1,y1) adalah:
dari soal di atas maka dapat dirinci menjadi:
x1 = -5
y1 = 4
m = -3
sehingga:
y - y1 = m (x - x1)
y - 4 = -3 (x - (-5))
y - 4 = -3 (x + 5)
y - 4 = -3.x + (-3).5
y - 4 = -3x - 15
y = -3x - 15 + 4
y = -3x - 11
bentuk di atas dapat diubah menjadi:
Selesai...
Rumus umum mencari persamaan garis dengan gradien m pada titik (x1,y1) adalah:
y - y1 = m (x - x1)
dari soal di atas maka dapat dirinci menjadi:
x1 = -5
y1 = 4
m = -3
sehingga:
y - y1 = m (x - x1)
y - 4 = -3 (x - (-5))
y - 4 = -3 (x + 5)
y - 4 = -3.x + (-3).5
y - 4 = -3x - 15
y = -3x - 15 + 4
y = -3x - 11
bentuk di atas dapat diubah menjadi:
y +3x = - 11
Selesai...
9. Titik (3, 4) dilalui persamaan garis ....
Kunci jawaban : tidak ada jawaban yang benar
Pembahasan:
Masukkan titik (3,4) ke masing-masing persamaan dengan x = 3 dan y = 4.
Tidak ada salah satu persamaan pun yang memenuhi. berikut buktinya:
A. 4x + 2y = -6 -> 4.3 + 2.4 = -6 -> 12 + 8 = -6 -> 20 = -6 -> kedua ruas tidak sama.
B. 4x - 2y = -6 -> 4.3 - 2.4 = -6 -> 12 - 8 = -6 -> 4 = -6 -> kedua ruas tidak sama.
C. 4x + 2y = -6 -> sama dengan A
D. 4x - 2y = -6 -> sama dengan B
karena kedua ruas sama maka (-5,5) dilalui oleh garis 3x + 2y = -5.
Masukkan titik (3,4) ke masing-masing persamaan dengan x = 3 dan y = 4.
Tidak ada salah satu persamaan pun yang memenuhi. berikut buktinya:
A. 4x + 2y = -6 -> 4.3 + 2.4 = -6 -> 12 + 8 = -6 -> 20 = -6 -> kedua ruas tidak sama.
B. 4x - 2y = -6 -> 4.3 - 2.4 = -6 -> 12 - 8 = -6 -> 4 = -6 -> kedua ruas tidak sama.
C. 4x + 2y = -6 -> sama dengan A
D. 4x - 2y = -6 -> sama dengan B
karena kedua ruas sama maka (-5,5) dilalui oleh garis 3x + 2y = -5.
10. Gradien garis yang melalui titik (1, 2) dan titik (3, 4) adalah ....
Kunci jawaban : 1
Pembahasan:
(x1,y1) = (1,2)
(x2,y2) = (3,4)
Gradien = y2-y1/x2-x1 = (4 - 2)/(3-1) = 2/2 = 1
(x1,y1) = (1,2)
(x2,y2) = (3,4)
Gradien = y2-y1/x2-x1 = (4 - 2)/(3-1) = 2/2 = 1
11. Persamaan suatu garis yang melalui titik (1, 2) dan titik (3, 4) adalah ....
Kunci jawaban : y = x + 1
Pembahasan:
(x1,y1) = (1,2)
(x2,y2) = (3,4)
Gradien (m) = y2-y1/x2-x1 = (4 - 2)/(3-1) = 2/2 = 1
Persamaan garis yang melalui (x1,y1) = (1,2) dengan m = 1 adalah:
y - y1 = m (x - x1)
y - 2 = 1 (x - 1)
y - 2 = x - 1
y = x - 1 + 2
y = x + 1
Selesai...
(x1,y1) = (1,2)
(x2,y2) = (3,4)
Gradien (m) = y2-y1/x2-x1 = (4 - 2)/(3-1) = 2/2 = 1
Persamaan garis yang melalui (x1,y1) = (1,2) dengan m = 1 adalah:
y - y1 = m (x - x1)
y - 2 = 1 (x - 1)
y - 2 = x - 1
y = x - 1 + 2
y = x + 1
Selesai...
12. Persamaan garis yang melalui titik (3, 6) dan sejajar dengan garis 2y + 2x = 3 adalah ....
Kunci jawaban : y = -x + 9
Pembahasan:
Persamaan garis yang melalui titik (3, 6) sejajar dengan garis 2y + 2x = 3 maka kemiringan (m) bernilai sama, sehingga:
2y + 2x = 3 -> 2y = -2x + 3 -> y = (-2x + 3)/2 -> y = (-2/2)x + 3/2 -> y = -x + 3/2 -> m = -1
jadi garis yang melalui titik (3, 6) memiliki m = -1.
Persamaan garis yang melalui (x1,y1) = (3,6) dengan m = -1 adalah:
y - y1 = m (x - x1)
y - 6 = -1 (x - 3)
y - 6 = -x + 3
y = -x + 3 + 6
y = -x + 9
Selesai...
Persamaan garis yang melalui titik (3, 6) sejajar dengan garis 2y + 2x = 3 maka kemiringan (m) bernilai sama, sehingga:
2y + 2x = 3 -> 2y = -2x + 3 -> y = (-2x + 3)/2 -> y = (-2/2)x + 3/2 -> y = -x + 3/2 -> m = -1
jadi garis yang melalui titik (3, 6) memiliki m = -1.
Persamaan garis yang melalui (x1,y1) = (3,6) dengan m = -1 adalah:
y - y1 = m (x - x1)
y - 6 = -1 (x - 3)
y - 6 = -x + 3
y = -x + 3 + 6
y = -x + 9
Selesai...
13. Persamaan garis yang melalui titik (-3,6) dan sejajar dengan garis 4y - 3x = 5 adalah ....
Kunci jawaban : tidak ada jawaban yang memenuhi
Jawaban alternatif : 4y = - 3x + 15
Pembahasan:
Persamaan garis yang melalui titik (-3, 6) sejajar dengan garis 4y - 3x = 5 maka kemiringan (m) bernilai sama, sehingga:
4y - 3x = 5 -> 4y = 3x + 5 -> y = (3x + 5)/4 -> y = (-3/4)x + 5/4 -> y = (-3/4)x + 5/4 -> m = -3/4
jadi garis yang melalui titik (-3, 6) memiliki m = -3/4.
Persamaan garis yang melalui (x1,y1) = (-3,6) dengan m = -3/4 adalah:
y - y1 = m (x - x1)
y - 6 = -3/4 (x - (-3))
y - 6 = -3/4 (x + 3)
y - 6 = (-3/4)x - 9/4
y - 6 = (-3x - 9)/4
4y - 24 = -3x - 9
4y = -3x - 9 + 24
4y = -3x + 15
Selesai...
Persamaan garis yang melalui titik (-3, 6) sejajar dengan garis 4y - 3x = 5 maka kemiringan (m) bernilai sama, sehingga:
4y - 3x = 5 -> 4y = 3x + 5 -> y = (3x + 5)/4 -> y = (-3/4)x + 5/4 -> y = (-3/4)x + 5/4 -> m = -3/4
jadi garis yang melalui titik (-3, 6) memiliki m = -3/4.
Persamaan garis yang melalui (x1,y1) = (-3,6) dengan m = -3/4 adalah:
y - y1 = m (x - x1)
y - 6 = -3/4 (x - (-3))
y - 6 = -3/4 (x + 3)
y - 6 = (-3/4)x - 9/4
y - 6 = (-3x - 9)/4
4y - 24 = -3x - 9
4y = -3x - 9 + 24
4y = -3x + 15
Selesai...
14. Persamaan garis yang melalui titik (4, –3) dan tegak lurus dengan garis 4y – 6x +10 = 0 adalah ....
Kunci jawaban : tidak ada jawaban yang memenuhi
Jawaban alternatif : 3y + 2x = - 1
Pembahasan:
Persamaan garis yang melalui titik (4, -3) tegaklurus dengan garis 4y – 6x +10 = 0 maka kemiringan (m) kedua garis kalau dikalikan harus bernilai -1, sehingga:
4y – 6x +10 = 0 -> 4y = 6x - 10 -> y = (6x - 10)/4 -> y = (6/4)x - 10/4 -> y = 3/2x - 5/2 -> m1 = 3/2
kalau m2 adalah kemiringan garis yang melalui titik (4, -3) maka berlaku:
m1 x m2 = -1
3/2 x m2 = -1
m2 = -1 : (3/2)
m2 = -1 x (2/3) = -2/3
Jadi garis yang melalui titik (4, -3) memiliki m = -2/3.
Persamaan garis yang melalui (x1,y1) = (4,-3) dengan m = -2/3 adalah:
y - y1 = m (x - x1)
y - (-3) = -2/3 (x - 4)
y + 3 = (-2/3)x + 8/3
y + 3 = (-2x + 8)/3
3(y + 3) = -2x + 8
3y + 9 = -2x + 8
3y = -2x + 8 - 9
3y = -2x - 1
3y + 2x = - 1
Selesai...
Persamaan garis yang melalui titik (4, -3) tegaklurus dengan garis 4y – 6x +10 = 0 maka kemiringan (m) kedua garis kalau dikalikan harus bernilai -1, sehingga:
4y – 6x +10 = 0 -> 4y = 6x - 10 -> y = (6x - 10)/4 -> y = (6/4)x - 10/4 -> y = 3/2x - 5/2 -> m1 = 3/2
kalau m2 adalah kemiringan garis yang melalui titik (4, -3) maka berlaku:
m1 x m2 = -1
3/2 x m2 = -1
m2 = -1 : (3/2)
m2 = -1 x (2/3) = -2/3
Jadi garis yang melalui titik (4, -3) memiliki m = -2/3.
Persamaan garis yang melalui (x1,y1) = (4,-3) dengan m = -2/3 adalah:
y - y1 = m (x - x1)
y - (-3) = -2/3 (x - 4)
y + 3 = (-2/3)x + 8/3
y + 3 = (-2x + 8)/3
3(y + 3) = -2x + 8
3y + 9 = -2x + 8
3y = -2x + 8 - 9
3y = -2x - 1
3y + 2x = - 1
Selesai...
15. Garis yang melalui titik (5, –3) dan sejajar dengan garis yang mempunyai gradien 1/3 adalah ....
Kunci jawaban :
16. Garis yang melalui titik (5, –3) dan tegak lurus pada garis yang mempunyai gradien – 2/3 adalah ....
Kunci jawaban :
17. Persamaan garis lurus yang melalui titik (–2, –4) dan titik (–4, 3) adalah ....
Kunci jawaban :
18. Persamaan garis yang melalui titik (4, 6) dan sejajar dengan garis yang melalui titik (3, 4) dan titik (5, 1) adalah ....
Kunci jawaban :
19. Persamaan garis yang melalui titik (6, –4) dan sejajar dengan garis yang melalui titik (–7, –4) dan titik (5, –5) adalah ....
Kunci jawaban :
20. Persamaan garis yang melalui titik (0, 6) dan tegak lurus dengan garis yang melalui titik (–4, 5) dan titik (–3, 3) adalah ....
Demikian Kunci Jawaban Uji Kompetensi 4 Bab Persamaan Garis Lurus Matematika Kelas 8 Semester 1. Semoga bermanfaat.


No 17 mna jawabannya
BalasHapus